We have developed a platform to measure and visualize Normal Difference Vegetation indices using a low cost Camera and a DE2 board. This device was tested on building facades showing building moisture that can be related to the inhabitant health. In a different project we have studied around 17000 buildings in Beirut to build and energy model, the simulation was run on Azure. In this proposal we try to merge the two concepts/techniques.
Project Proposal
1. High-level project introduction and performance expectation
Urban expansion, driven by population and economic growth, has been a major contributor to the decrease in the daylight factor inside buildings and the increase of energy consumption for lighting to compensate for that. Besides, a usually ignored factor is the direct sun exposure of buildings that is decreasing in most urban areas. Moisture control is fundamental to the proper functioning of any building. Controlling moisture is important to protect occupants from adverse health effects and to protect the building, its mechanical systems and its contents from physical or chemical damage. Moisture monitoring is of primordial importance in any urban planning or urban management.
Using low cost image sensors controlled and driven by Altera-FPGA, we have shown that large area moisture scans can be done remotely. The highly demanding image processing part will be handled using GPU. We will use an already developed method. The methodology uses rule-based expert data for an archetypal classification of the buildings based on their functions and periods of construction with their corresponding attributes including the number of floors, number of apartments, and bimonthly electricity consumption to generate a 3D model for buildings coupled to the hourly weather conditions and topographic map, which is then simulated in EnergyPlus. The previously developed model uses already existing data; in this project we would like to develop live simulation using Intel technology.
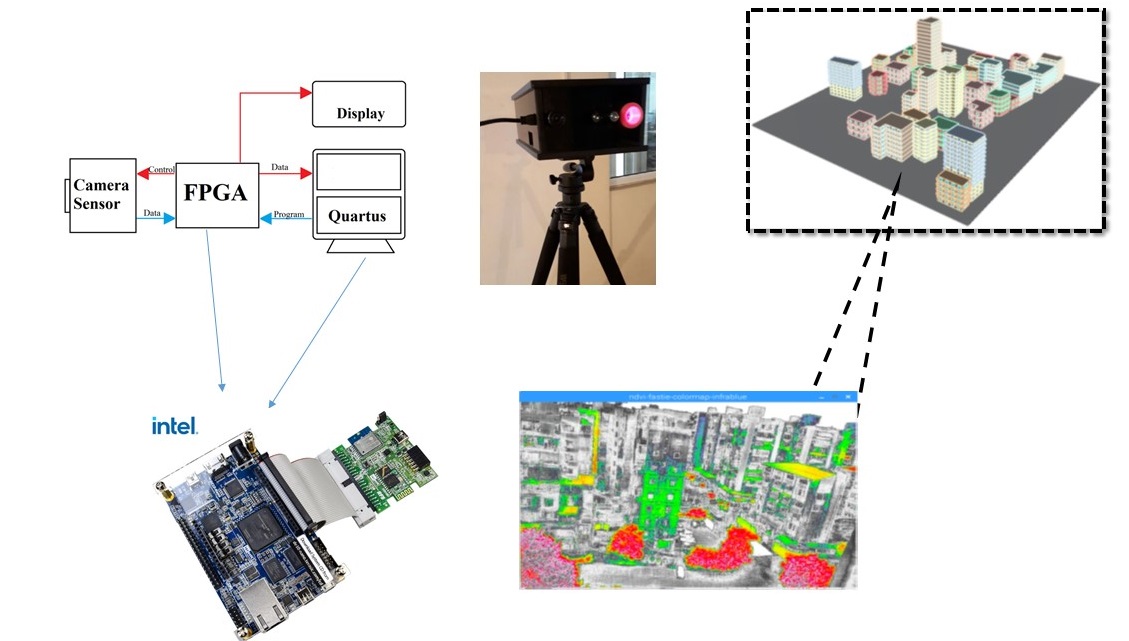
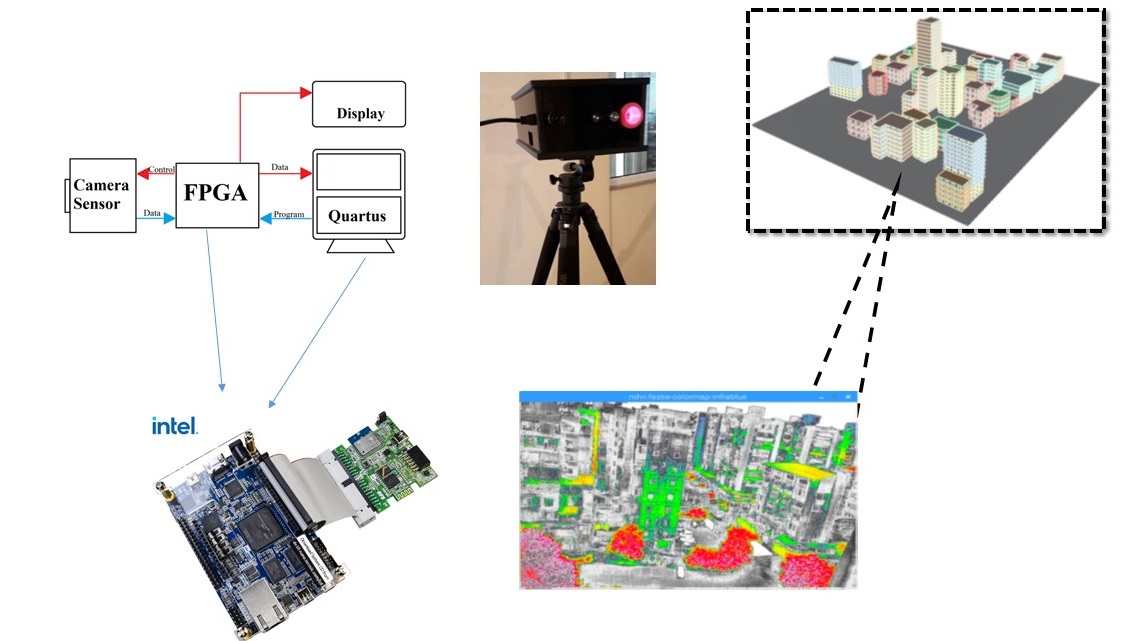
2. Block Diagram
3. Expected sustainability results, projected resource savings
- Megapixel buffering
- On-board image processing
- Hundredth of buildings data acquisition
- Fast data trasmittion via Ethernet port
- ML algorithms run on cloud
4. Design Introduction
In our previous tests we have tested
- Altera FPGA with a low cost OV camera
- Raspberrypi with NOIR camera
FPGA board was programmed to drive OV camera and get raw image which is sent serially via RS232 port. The captured images have been processed externally. In both projects, moist regions and algae has been successfully detected.
We will try to develop both solutions, the Pi-solution is for the ease of use, however for robustness we developed the FPGA solution.
5. Functional description and implementation
The sensor used in this first design was a low cost OV7670 camera with no IR blocking filter in front of the sensor. The control of the camera was done using an Altera DE2 FPGA board using a Verilog-HDL developed code. The control allow for a raw format without any interpolation. The processing is then done in a first stage on a PC. Now we would like to do all the processing onboard. We have to process two images and send a single final NDVI mapped image to the Ethernet port. We would like also to explore validation of our design with the Analog Devices evaluation board EVAL-CN0397-ARDZ in the red channel.
6. Performance metrics, performance to expectation
In the actual design it was not possible to transmit data fast enough since data rate transmission of serial port is limited. This also limits the ability to get enough frames per second from the camera keeping the design far from video processing or even large scale image processing. In the new project high speed data transmission is the most important part in addition to onboard NDVI processing that should be made.
Intel FPGA board is the most proper choice for our design since it has additional gates and wiring that allow it to be flexible and programmable and it is ideal for real time applications as it can perform more processing in a shorter period of time as compared to other alternatives in market.
7. Sustainability results, resource savings achieved
Previous software flow:
1. Clock is sent to the camera to get parallel 8 bit pixel
2. Data are saved in six RAMs
3. Data are sent serially using Rs232 port to Matlab
Camera is controlled by calling the addresses referring to the data sheet.
On top of this we have to develop the Ethernet communication part in addition to onboard processing then data transmitted from FPGA board is only the NDVI ratio or more necessary data.
8. Conclusion
We would like to develop a low cost external building moisture mapping together with full scale urban modeling to assist decision maker in adding new legislation respecting the quality of life and building health.
0 Comments
Please login to post a comment.