PR089 » 無線定位之FPGA設計與實現
隨著智慧型手機的普遍，定位系統亦透過手機大大提升了普遍率，並廣泛地在許多產業中發展，因此有了定位技術。定位技術是行動計算重要的基礎，透過行動載具 (手機) 便能提供位置感知計算的服務以及即時位置相關的資訊給使用者。Kalman Filter (KF) 具有處理模型誤差、測量雜訊以及提升定位系統之精確度之特性，因此本計畫將以 KF 為基礎作為定位的處理機制。本計畫將使用 Field-Programmable Gate Array (FPGA) 實現用於位置追蹤的 KF 演算法，設計與實現 KF 定位演算法將分成幾項部分探討：第一部分為 KF、FPGA 之理論基礎；第二部分為 KF 參數之調整以提高準確度；第三部分為利用 KF 演算法設計的 IC 模型。綜上所述，我們將先了解 KF 之特性，並以此為結果作為未來改善定位系統之前導研究，期以提升定位系統之準確度。定位技術是行動運算中重要的一環,它可以讓移動中的使用者取得即時資訊。本研究計畫將嘗試依環境的不同， 根據演算法算出精確的位置，並將其應用於具有適地性服務 (Location-Based Service，LBS) 應用的平台上。以 FPGA 實現 KF 定位追蹤演算法具有即時定位的特性，以位置資訊為基礎的行動運算可以讓使用者隨時隨地獲得各種資訊各種資源，此研究成果將可延伸應用於醫療、交通、旅遊、娛樂、文化、智慧網路等以 LBS 為基礎的應用系統之相關領域。
介紹
鑒於現今無線通訊的快速發展、網路技術的突飛猛進，自駕車和無人飛行載具的快速崛起，定位系統的應用已經無所不在，定位系統的準確度和運算複雜度一直是定位系統的兩大挑戰。現今大多數的定位系統是使用軟體實現，軟體實現會導致速度延遲，造成無法滿足適地性服務 (LBS，location-based service) 的即時應用需求。為了提高定位系統的準確度，可以將 KF (Kalmen filter) 的資料融合演算法應用到定位系統。為了提高演算法的運算速度，已經有許多改進的方法被提出。其中簡化的 KF (Kalmen filter) 演算法，雖然可以大幅提高處理速度，但會降低定位演算法的可適性以及精確度。使用傳統 KF 演算法的異質資料融合定位技術需要反覆計算反矩陣，反矩陣運算會產生相對較高的運算複雜度，運算複雜度過高的演算法通常不適合直接應用在即時系統中。在實際的應用系統中， KF 演算法通常由數位訊號處理 (DSP, digital signal processing) 的處理器來實現， DSP 處理器是依照 CPU 架構的方式執行程序的順序，KF 演算法需要處理大量的矩陣運算，現今採用 DSP 的程序仍無法滿足系統高速、即時的需要。
優勢
使用 FPGA 實行 KF 演算法具有高速算術功能與管線化的優點，因此，FPGA 的高可移植性、高精度以及易於開發的特性將可擴展 KF 在 LBS 即時應用的領域。KF 演算法的計算量比較大，當取樣率比較高的時候，一個取樣週期內難以完成計算，且計算機的運算位元有限，使得計算中產生捨入誤差以及截斷誤差的累積、傳遞，造成微控制器和 DSP 難以實現。採用 FPGA 實現 KF，輸入和輸出數據的計算可以同時進行，將可大幅提高 KF 演算法的濾波速度。
應用
KF 演算法可應用在許多系統中，以 FPGA 實現 KF 定位追蹤為基礎的異質資料融合方法除了用於無線通訊系統的通道訊號追蹤，更可延伸應用於經濟學、動態定位系統、自駕車、衛星導航、慣性導引以及雷達跟蹤等系統。
1. 在定位系統中， KF 演算法的運算速度跟精確度是定位應用中是否成功的關鍵，本計畫使用 FPGA 硬體技術實現 KF 異質資料融合演算法，以提高位置追蹤的運算速度。
2. FPGA 硬體實現具有高可移植性、高精度、低成本與容易擴展系統的優勢，從 MATLAB 模型直接應對 FPGA 硬體設計的 KF 演算法擺脫了傳統實現系統對平台的依賴性，此方法可以增加系統的靈活性以及實現的效率。
3. Table I是取樣100個位置資料使用KF追蹤演算法所花的時間，左欄代表MATLAB軟體的完成時間，而右欄代表FPGA硬體的完成時間，從Table I的結果得知使用FPGA硬體方法的速度比軟體方法的速度提高了34倍。
現今定位系統的應用已經無所不在，而定位系統的準確度和運算複雜度一直是定位系統的兩大挑戰。 此演算法的概念是使用遞迴的關係式，也就是一層一層去推算，求得出結果亦不需儲存大量數據，也便於在計算資料上使用。以FPGA實現KF演算法位置追蹤演算法，輸入和輸出數據的計算是同時進行，可以大幅提高KF演算法的速度。傳統KF演算法的資料融合技術需要反覆計算反矩陣，反矩陣運算產生高的運算複雜度，初期的目標為解構KF演算法的矩陣，使其在運用上更為簡化，並將其應用於FPGA或IC設計上。
此成果可應用於導航、航空、機器人、自駕車、無人飛行載具、圖像處理、語音處理、天氣、地質探勘、故障診斷等系統以及計量經濟學，只要和時間序列有關和高斯分布就能建立相關的模型，並且作為線性動態系統的輸入和輸出，無論是平穩隨機訊號或是隨機複雜訊號，只要知道訊號的時域，就可利用KF演算法處理雜訊，估計出原本想要的訊息，用來預測和濾波出需要的結果。KF演算法可以透過現時刻有限又有雜訊的訊號，配上KF演算法前一刻的估計量，求出現時刻中我們想要的原訊號以及估計量作為下次輸入，意即在有限的訊號條件下，例如當我們只知道物體的位置，KF演算法只需利用位置訊息即可還原出速度量，然而在對應不同的動態系統時，只需調整相關的幾個參數即可以運用KF演算法去處理不同的領域，可以說十分靈活。
KF演算法為利用在時域與狀態空間的概念，分成預測狀態和修正狀態，並分成四大運算式，上圖流程循環圖的參數如下：
以及
分別是狀態估測矩陣以及狀態預測矩陣；
以及 
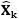
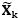
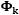
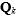分別是狀態轉移矩陣以及模型雜訊協方差矩陣；
、
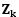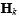以及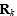
分別是實際量測矩陣、量測轉移矩陣以及量測雜訊協方差矩陣；
、
以及
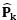
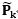
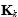分別是估測誤差協方差矩陣、預測誤差協方差矩陣以及卡爾曼增益 (Kalman gain, KG)；
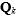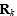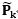
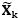
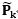
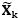
其中的是由該系統的長期估計下來的協方差構成，則是信號傳輸過程中所導致的協方差構成，對應不同的動態系統需要變動這兩個參數去配合KF演算法，對於和會造成影響，而和作為每一次迴圈的輸入。
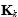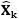
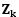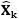
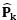
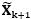
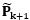
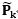
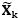
首先計算出了增益，再來矩陣也就是我們想從中從有雜訊的訊號想得到的原訊號，包含了訊號的位置以及速度，也就是我們從雜訊中留下想要的訊號，接著求得矩陣，最後則利用前面三個式子去得到
和
並作為下一次的迴圈輸入，也就是作為下一次輸入的和，雜訊的數量將決定遞迴的圈數。
而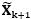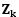和兩者的相關方程式，可以用狀態空間模型來表示，其結果如下(1)到(4)式所述：
(2)式為(1)式之數學式的矩陣表示式
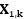
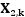
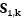以及
分別是 x 以及 y 方向的位置；
以及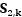
分別是 x 以及 y 方向的速度；
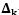是取樣的時間；
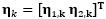是移動狀態的處理雜訊；
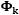
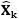
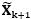
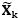
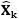
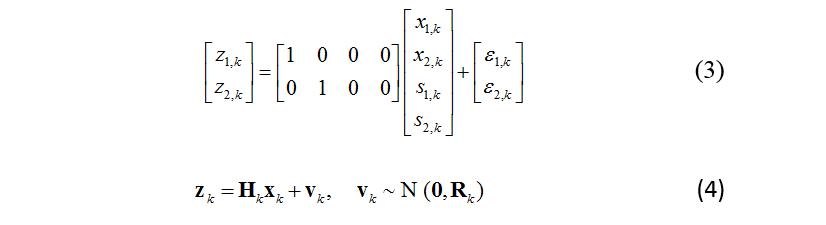
運用和此刻的算出做為下一個遞迴週期的，對於計算出流程圖中的相當重要，而(2)式即可代表出預測狀態(Prediction State)。
(4)式為(3)式之數學式的矩陣表示式，其中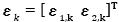
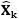
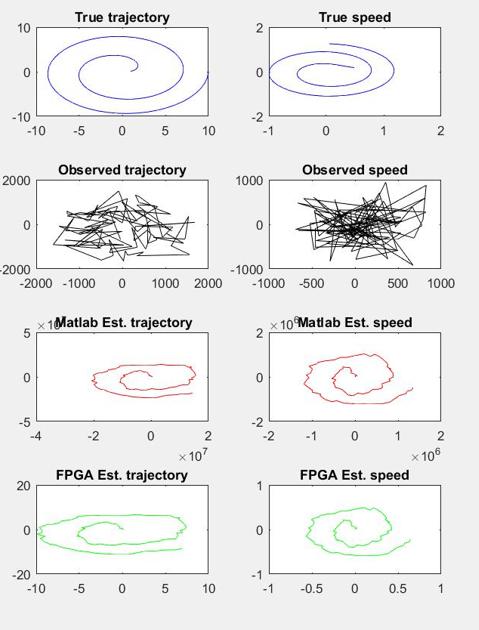
為量測狀態的處理雜訊；而(4)式對於計算出流程圖中的也十分重要，是構成修正狀態 (Correction State) 中重要的一環。
而下圖為KF演算法透過Matlab展示之結果:
True trajectory為原始訊號的位置圖；
Ture speed為原始訊號的速度圖；
Observed trajectory為原始訊號加上雜訊的位置圖；
Observed speed為原始訊號加上雜訊的速度量圖；
Matlab Est.trajectory為軟體實踐KF演算法還原雜訊訊號後的位置圖；
Matlab Est.speed為軟體實踐KF演算法還原雜訊訊號後的速度量圖；
FPGA Est.trajectory為硬體實踐KF演算法還原雜訊訊號後的位置圖；
FPGA Est.speed為硬體實踐KF演算法還原雜訊訊號後的速度量圖；
由原始圖跟FPGA還原後的圖比較可觀察出還原率相當高。
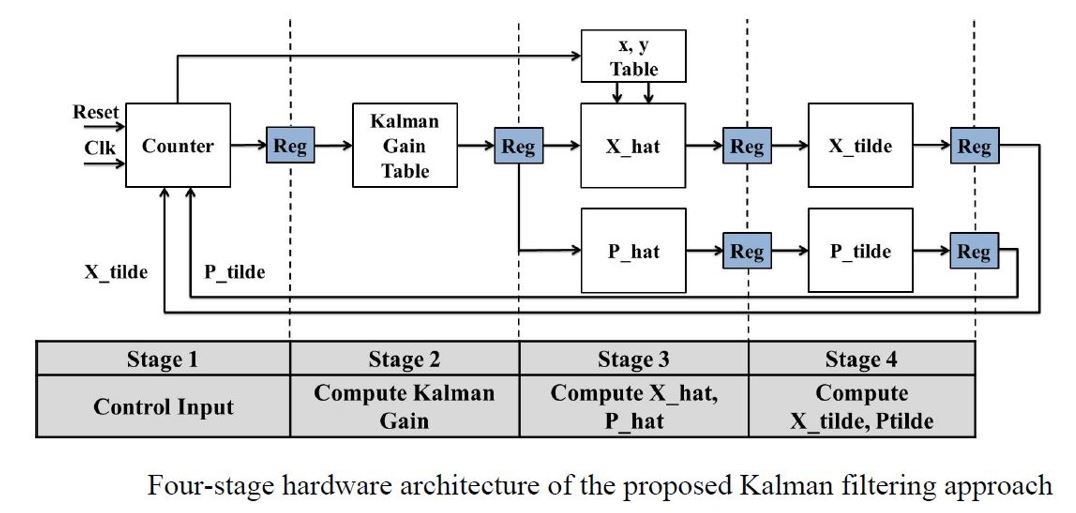
Hardware Design Block Diagram
Software flow
