

PR137 » 基于视觉的三维图像重建
我们的目标在于设计一个三维建模系统并安装在无人机系统上以达到能在高空中对大面积地形进行全自动化三维模型构建、形成三维真实场景。
我们提出使用无人机三维建模技术,是因为近年来,消费级旋翼无人机的市场逐渐做了起来,买一个到手就能飞的相机已经是一件非常现实的事情,而在这种条件下,譬如面对各国的位于高山丘陵的自然风景区,使用无人机可以快速得到景区三维鸟瞰图,获得景区的相关信息数据,从而对环境复杂、地形陡峭的自然景区进行完美的规划和设计,达到巧夺天工、浑然天成的理想设计目标。
使用这种技术来对城市进行高空三维建模,构造出的三维城市模型可以使人们摆脱传统的二维平面地图的束缚,使人们对城市景观的现状和设计结果有十分直观的印象,打个比方,经过这种技术处理后,我们能够在虚拟世界中看到大城市的建筑都是立体的,可以看到房子的高度信息,在3D视角下自由移动,从而能够在虚拟世界中欣赏到城市的地貌景观,导航定位更加直观,或是可以对城市的规划设计做一些评估、改进等等。
目标:我们想要设计出一个基于FPGA的无人机航拍三维建模系统三维设计经过多年来的发展,已在各行业中广泛使用在工程设计越来越激烈的市场竞争中,随着人们对视觉要求的不断提高,对产品的质量也提出了更高的要求,不仅需要满足农业,工业,旅游业等等的设计需求,提高设计的效率,同时又需要增加三维展示地面地物的贴图渲染,以达到工程设计和产品展示的三维视觉双重效果,以提高市场竞争力。近年来,随着测绘科技的发展,遥控无人飞机低空航空摄影测绘技术的日趋成熟,在测绘中具有非常重要的作用,无人飞机航测通常低空飞行,受气候条件影响较小,系统携带的数字彩色航摄相机等设备可快速获取地表信息,获取超高分辨率数字影像和高精度定位数据,拍摄影像清晰,分辨率高,现势性好,用于地形图测绘和制作三维模型 效果良好。我们希望两者结合,通过FPGA完成,做出一款线路简单,数据传输更快,逻辑可随意修改,应用范围更广的智能产品。
应用:无论是无人机,还是三维设计在当前都是具有很大的需求市场我们希望利用FPGA的高速,安全,灵活性强等特点,充分展示FPGA强大的优势无人机三维建模系统将可以广泛用于城市规划设计,土地林地布局设计等用途,如构造三维城市模型,获得景区,土地三维鸟瞰图而进行规划工作等。
目标用户:我们的目标用户领域包括工业,农业,旅游业领域等等目前,虽然对航拍三维建模的需求愈发剧烈,但是针对用户行为分析理解的产品少之又少,大量使用高性能GPU和NPU造成的巨额成本严重阻碍产品的推广,降低成本又无法满足算法复杂度的要求.FPGA在人工智能领域的使用是对GPU和NPU需求的响应.FPGA在该领域的应用会引起新的一轮技术竞技。
应用程序接口:为了系统的正常运行和实时接收航拍数据并正常发送控制信号,我们需要在PC终端设计一款系统信息软件,该软件能接受系统各类反馈信息并能实时控制系统,为系统提供良好的用户总控制界面。
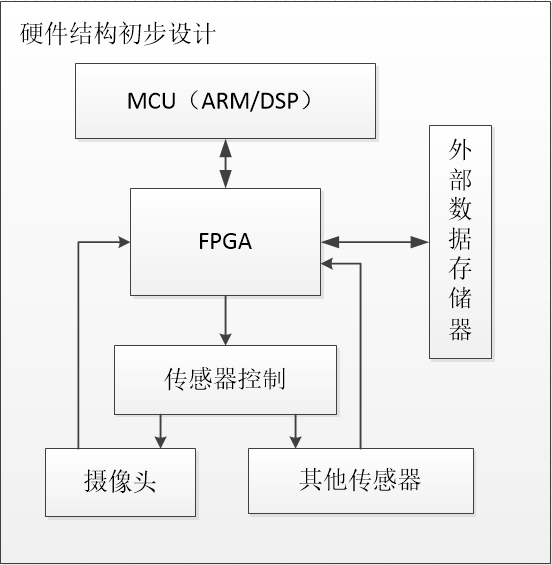
高集成度,使得线路简单,占空间小: FPGA要担任整个系统的核心,他完成的的工作包括高速接口设计,算法处理等。完成对无人机控制信号信号的发送接收,以及航拍图像信号的采集、处理、储存和读取功能。由于结构较多,如果像平常使用各类芯片完成各项逻辑会使得线路十分复杂,系统成型后所占空间也会变大。FPGA的电路式并行操作给我们提供了线路复杂的解决方案,所以FPGA成为我们系统最优秀的硬件设计。另一方面,我们需要FPGA与PC终端的软件提供接口交互,允许上位机对系统进行操作,FPGA不仅要完成解析上位机软件命令的任务,还需要完成统筹外围硬件的在线状态,对每一个硬件模块实施即时性操作。
数据采集处理速度快:我们可以利用FPGA对无人机和建模数据进行采集,并对这些复杂的的信号进行前期的预处理,包括数据统计、滤波降噪、信号裁剪和信号调制,然后将处理完成的信号分别存入SDRAM中。FPGA能够高速采集和处理得到我们需要的数字信号,还可以达到混频的效果,为下一级处理提供时钟匹配。
抗干扰能力强:由于控制信号和图像容易受到外部干扰,一般的采集方式都会混入大量的噪声信号,严重降低了信号的信噪比,甚至出现淹没信号的情况。使用FPGA技术,只要设计得当,其电路式的采集处理过程都具有极大的稳定性,大大提高了有用信号的功率。同时我们也需要使用FPGA对系统进行加密,禁止除授权用户外所有人的篡改系统,FPGA的使用大大的增加了破解系统的难度,为系统的安全提供了优秀的保障。
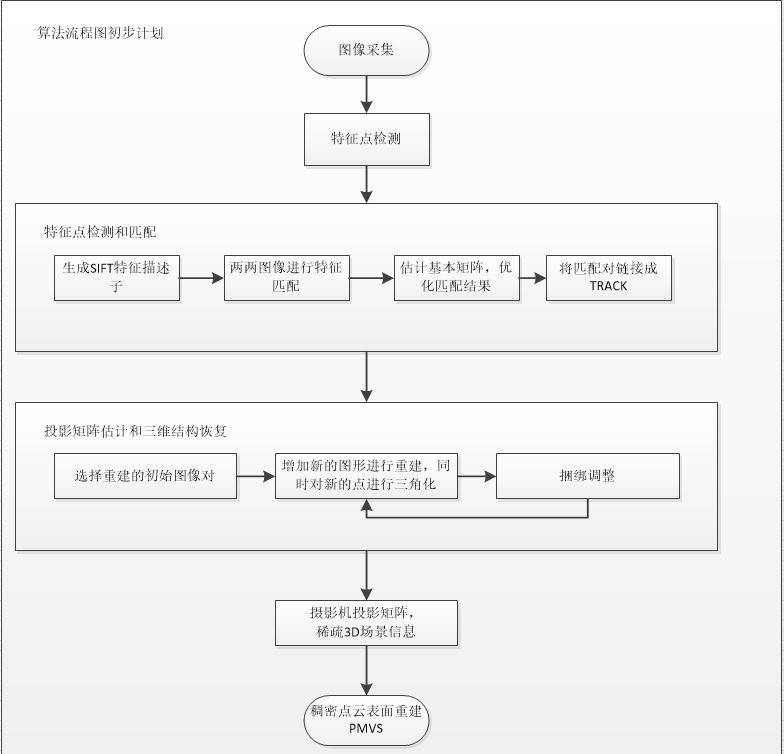
基于立体视觉的室外大规模场景三维重建,一直以来是国内外研究的热点与难点问题。针对此问题近几年来主要用:影像金字塔、SIFT算法、BRISK算法等方法来解决。本设计拟采用SIFT算法来解决问题。对于某些特征不明显、纹理信息不明显的场景,其检测的特征点数量较少,且重建出的模型不完整,故不能将SIFT算法直接应用于这些场景的三维重建。伴随着无人机技术的兴起和民用化,结合多视图三维重建技术。利用Harris特征检测结合SIFT特征检测,增加图像特征点数量,采用成熟的Bundler算法和CMVS /PMVS 算法,获得稠密点云信息,且对点云信息进行网格化和纹理映射,最终能得到真实的场景信息。
为了达到目的,基于官方提供的开发板,我们已经能够实现对室内拍摄下来的一些物体进行三维重建。具体实现方法将在下文中详细介绍。
(1)单目标定
在图像测量过程以及机器视觉应用中,为确定空间物体表面某点的三维几何位置与其在图像中对应点之间的相互关系,必须建立相机成像的几何模型,这些几何模型参数就是相机参数。在大多数条件下这些参数必须通过实验与计算才能得到,这个求解参数的过程就称之为相机标定(或摄像机标定)。无论是在图像测量或者机器视觉应用中,相机参数的标定都是非常关键的环节,其标定结果的精度及算法的稳定性直接影响相机工作产生结果的准确性。因此,做好相机标定、提高标定精度是做好后续工作的前提,是我们科研工作的重点所在。
为了进行单目标定,我们通过查阅资料了解到目前相机标定的主流方法是张正友标定法。这种方法通过对一定标板在不同方向多次(三次以上)完整拍照,不需要知道定标板的运动方式。直接获得相机的内参和畸变系数。该标定方法精度高于自定标法,且不需要高精度的定位仪器。张正友标定法包含两个模型:经典针孔模型,包含四个坐标系,以及畸变模型。首先,对于张正友算法的标定点选取,一般是选择能均匀分布于整个图像的一些点。对于相机的标定精度而言,选取的点越多,反应图像的信息越完整,因而得到的结果越好。但是随着点数的增加,其运算量增加,同时增加点数带来精度提高的效果随着点数增加而逐渐减弱。我们选用了11*8的标定棋盘格对相机进行标定。
bool findChessboardCorners( InputArray image, Size patternSize,OutputArray corners,
int flags=CALIB_CB_ADAPTIVE_THRESH+CALIB_CB_NORMALIZE_IMAGE );
使用findChessboardCorners函数提取角点,这里的角点专指的是标定板上的内角点,这些角点与标定板的边缘不接触。
void cornerSubPix( InputArray image, InputOutputArray corners,Size winSize, Size zeroZone, TermCriteria criteria );
为了提高标定精度,需要在初步提取的角点信息上进一步提取亚像素信息,降低相机标定偏差,这里使用的方法是cornerSubPix。void drawChessboardCorners( InputOutputArray image, Size patternSize,
InputArray corners, bool patternWasFound );
drawChessboardCorners函数用于绘制被成功标定的角点。double calibrateCamera(InputArrayOfArrays objectPoints,InputArrayOfArrays imagePoints,
Size imageSize,CV_OUT InputOutputArray cameraMatrix,
CV_OUT InputOutputArray distCoeffs, OutputArrayOfArrays rvecs,
OutputArrayOfArrays tvecs, int flags=0,TermCriteria criteria =
TermCriteria( TermCriteria::COUNT+TermCriteria::EPS, 30, DBL_EPSILON) );
获取到棋盘标定图的内角点图像坐标之后,就可以使用calibrateCamera函数进行标定,计算相机内参和外参系数。
标定过程部分图如下:

进行编译后,得到的结果如下:
左相机内参数矩阵:
[818.1427496880933, 0, 323.0385178639263;
0, 817.9300827874146, 240.8374341990319;
0, 0, 1]
左相机畸变系数:
[0.007972794169599078, 0.9671128656101282, -0.004508405370384771, -0.003759170785283997, -3.974751183062043]
右相机内参数矩阵:
[817.7062598353203, 0, 315.0602094509645;
0, 818.1971497220782, 251.3193229387233;
0, 0, 1]
右相机畸变系数:
[-0.03106127369807768, 1.179919498442583, -0.00365980799250647, -0.002709688952785218, -3.716696603639026]
在计算机视觉中,若要评价相机标定结果的数值是否精确,最常用的评价标准便是重投影误差。在标定过程中,计算平面单应矩阵和投影矩阵的时候,往往要使用重投影误差来构造代价函数,然后最小化这个函数,来对结果进行优化。重投影误差不但考虑了单应矩阵的计算误差,也考虑了图像点的测量误差,所以将重投影误差作为标定结果的评价标准,会更为直观的测出标定结果精确度的高低。
从物体到平面的映射,同时表征了两个平面的相对位置和相机投影矩阵,即外参和内参。
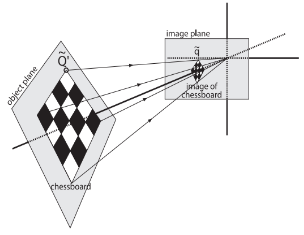
以平面单应矩阵的计算为例,假设两幅图像中的对应点满足:
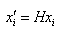
其中,H是平面单应矩阵,x和x’是图像中的对应点,则重投影误差的形式如下:
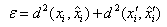
最小化重投影误差就是优化H和x两个值。从重投影误差公式可以看出,模型认为测量点并非绝对精确,而是存在一定的测量误差,因此需要重新估计图像点的坐标,而估计得到的新的图像点之间完美的满足单应关系。下图就是重投影误差的几何表述,d和d’的和即为重投影误差:
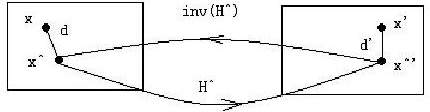
为了验证我们通过张正友标定法得到结果的精确度,我们还使用了Matlab对我们的25张标定板图片进行标定以及计算重投影误差。
通过在Matlab提取点信息,可以将映射误差显示在图中,离中心越远,说明误差越大:
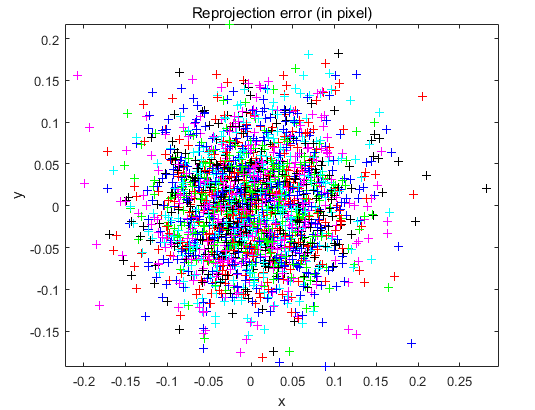
下图中,坐标系(Oc,Xc,Yc,Zc)是相机的参考坐标系。红色的金字塔状的就是由图像平面定义的相机的有效视场。
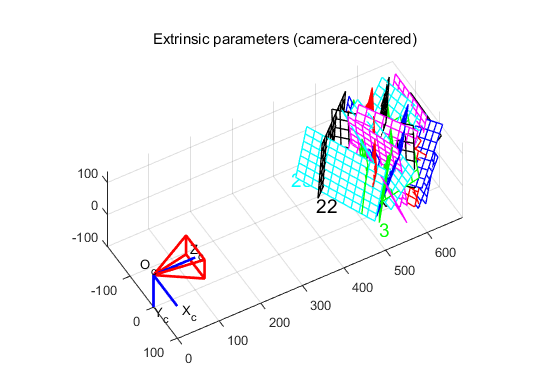
可以在相机坐标系视角或者世界坐标系视角之间切换(在这个视角里面,每个相机的位姿都用绿色的金字塔表示):
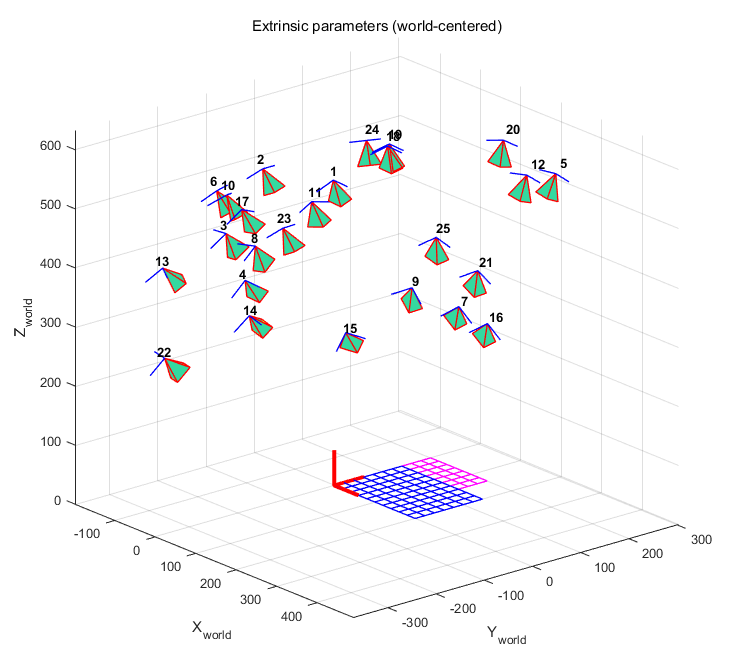
通过鼠标点击选取一个误差比较大的点,我们可以看到这个点出自于哪张图片,以及误差具体信息等等:
选取误差较大点:
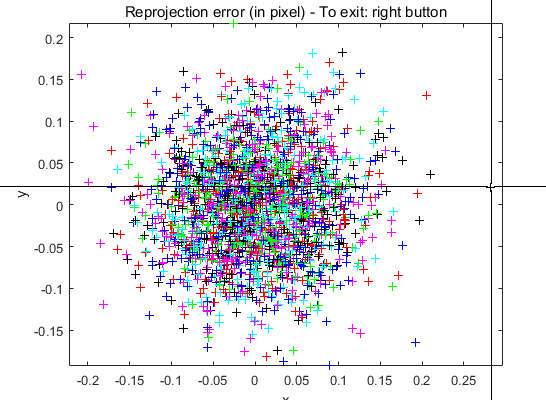
误差较大点的来源以及位置信息:
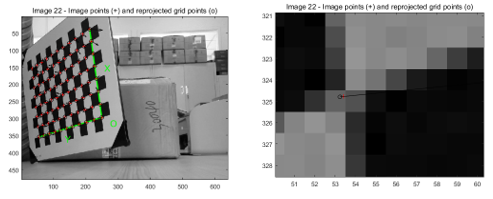
为了选择合理的畸变模型来使用,通常可视化对像素图像的畸变影响以及畸变的径向部分和切向部分的比对是非常有用的。为此,matlab命令行运行visualize_distortions,就会有三张图出来:
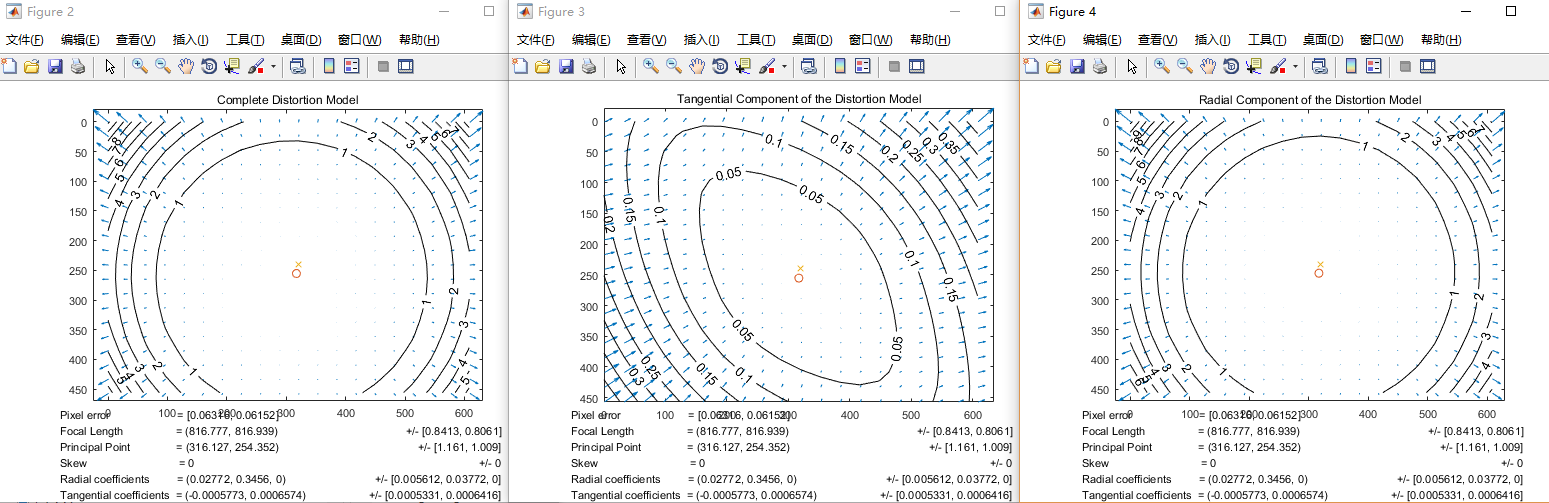
第一幅图显示了整体的畸变模型对图像每个像素的影响。每个箭头表示由于镜头畸变而使一个像素发生的位移效果。
第二幅图显示了畸变的切向部分。
最后,第三幅图显示了畸变的径向部分的影响。在第三幅图中,十字叉表示了图像的中心,而圆表示光心所在的位置。
以下是通过Matlab标定出的内参结果:

可以看出,Matlab的标定结果与张正友标定法的标定结果相差无几,所以我们这里选择使用张正友标定法来对每个相机进行标定。
(2)双目标定
完成单目标定后,我们能分别得到两个相机各自的内参,但是还没有得到两个相机之间的位置关系相关的数据,也就是外参。所以接下来就需要通过双目标定得到相机组的外参。双目标定的第一步需要分别获取左右相机的内外参数,之后通过立体标定对左右两幅图像进行立体校准和对其,最后就是确定两个相机的相对位置关系,即中心距。
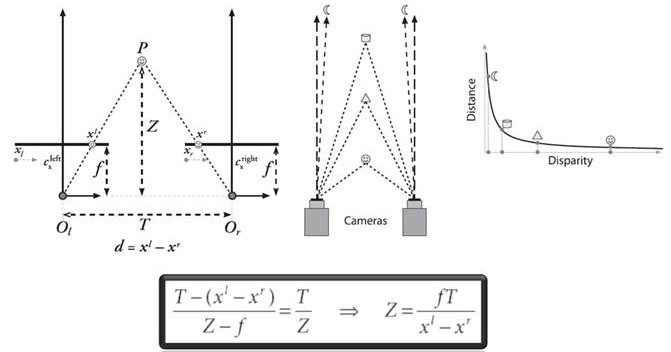
假设有一个点p,沿着垂直于相机中心连线方向上下移动,则其在左右相机上的成像点的位置会不断变化,即d=x1-x2的大小不断变化,并且点p和相机之间的距离Z跟视差d存在着反比关系。上式中视差d可以通过两个相机中心距T减去p点分别在左右图像上的投影点偏离中心点的值获得,所以只要获取到了两个相机的中心距T,就可以评估出p点距离相机的距离,这个中心距T也是双目标定中需要确立的参数之一。
FindChessboardCorners( const void* image, CvSize pattern_size, CvPoint2D32f* corners,
int* corner_count = NULL, int flags = CV_CALIB_CB_ADAPTIVE_THRESH )
FindChessboardConers用于寻找棋盘图中棋盘角点;
cvDrawChessboardCorners( CvArr* image, CvSize pattern_size, CvPoint2D32f* corners,
int count, int pattern_was_found )
cvFindChessboardCorners()发现所有角点绘制到所提供的图像上;
void cornerSubPix( InputArray image, InputOutputArray corners, Size winSize,
Size zeroZone,TermCriteria criteria )
在角点检测中精确化角点位置;
double stereoCalibrate(InputArrayOfArrays objectPoints,
InputArrayOfArrays imagePoints1, InputArrayOfArrays imagePoints2,
InputOutputArray cameraMatrix1, InputOutputArray distCoeffs1,
InputOutputArray cameraMatrix2, InputOutputArray distCoeffs2,
Size imageSize, OutputArray R, OutputArray T, OutputArray E, OutputArray F,
TermCriteria criteria=TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 30, 1e-6),
int flags=CALIB_FIX_INTRINSIC )
双目摄像机标定,计算了两个摄像头进行立体像对之间的转换关系,根据左右相机的参数矩阵,生成两个相机之间的关系矩阵,以及基本和本质矩阵。
cvCalibrateCamera2( CvMat* object_points, CvMat* image_points, int* point_counts,
CvSize image_size, CvMat* intrinsic_matrix, CvMat* distortion_coeffs,
CvMat* rotation_vectors = NULL,CvMat* translation_vectors = NULL, int flags = 0 );
利用定标来计算摄像机的内参数和外参数;
cvFindExtrinsicCameraParams2(const CvMat* object_points,const CvMat* image_points,
const CvMat* intrinsic_matrix,const CvMat* distortion_coeffs,
CvMat* rotation_vector, CvMat* translation_vector );
计算摄像机外部参数。
双目标定·过程部分图如下:

得到的平移矩阵,旋转矩阵等重要外参参数如下:
旋转矩阵:[ 9.9965083506685637e-01, 8.1936834208969373e-03,
-2.5121136561367424e-02, -9.3036407385304592e-03,
9.9897093188196262e-01, -4.4390534169926173e-02,
2.4731563216770367e-02, 4.4608752581541046e-02,
9.9869835735019297e-01 ]
平移矩阵:[ -7.1041511229348060e+01, -1.2031693952366919e-01,
-1.9149503217364863e-01 ]
B.特征点提取以及立体匹配
SIFT是一种检测局部特征的算法,该算法通过求一幅图中的特征点及其有关规模和取向的描述子得到特征并进行图像特征点匹配,获得了良好效果,SIFT特征不只具有尺度不变性,即使改变旋转角度,图像亮度或拍摄视角,仍然能够得到好的检测效果。
首先构建尺度空间,这是一个初始化操作,尺度空间理论目的是模拟图像数据的多尺度特征,再寻找尺度空间的极值点,每一个采样点要和它所有的相邻点比较,看其是否比它的图像域和尺度域的相邻点大或者小。然后再将不好的特征点去除,通过拟和三维二次函数以精确确定关键点的位置和尺度,同时去除低对比度的关键点和不稳定的边缘响应点,以增强匹配稳定性、提高抗噪声能力。
 图5 特征点提取
图5 特征点提取
cornerSubPix(gray, corners, winSize, zeroZone, criteria)
此函数用于亚像素角点检测。
立体匹配是立体视觉研究中的关键部分。其目标是在两个或多个视点中匹配相应像素点,计算视差。通过建立一个能量代价函数,对其最小化来估计像素点的视差,求得深度。
当采取两个同一水平线上的摄像头进行拍摄的时候,同一物体将在两个摄像机内被拍摄到,在两个摄像机内部,这个物体相对于摄像机中心点位置有不同的坐标。我们假设Xleft是该物体在左摄像机内相对位置,Xright是该物体在右摄像机内相对位置,两个摄像机相距S,焦距为f,物体P距离摄像机z,z也就是景深。当我们将两幅图像重叠在一起的时候,左摄像机上P的投影和右摄像机上P的投影位置有一个距离|Xleft|+|Xright|,这个距离称为Disparity。
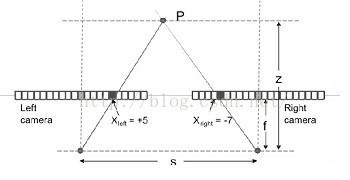
根据相似三角形可以得到z=sf/d. 也就是只要计算得到了d的值,就可以计算得到深度图。而在计算d的值的过程中需要对两幅图像进行匹配,寻找到物体P在两幅图像中的相对位置。在对图像进行匹配的过程中,需要用到cost computation,即通过寻找同一水平线上两幅图像上的点的最小误差来确定这两个点是否是同一个物体所成的像。由于一个点所能提供的信息太少,因此往往需要扩大对比的范围。
Opencv中立体匹配的算法主要有三种,分别是BM,SGBM和GC算法,SGBM算法得到的视差图相比于BM算法来说,减少了很多不准确的匹配点,尤其是在深度不连续区域,速度上SGBM要慢于BM算法。OpenCV3.0以后没有实现GC算法,可能是出于速度考虑,所以这里我们采用SGBM算法进行立体匹配。参数设置如下:
sgbm->setP1(8 * cn*sgbmWinSize*sgbmWinSize);
sgbm->setP2(32 * cn*sgbmWinSize*sgbmWinSize);
sgbm->setMinDisparity(0);
sgbm->setNumDisparities(numberOfDisparities);
sgbm->setUniquenessRatio(10);
sgbm->setSpeckleWindowSize(100);
sgbm->setSpeckleRange(32);
sgbm->setDisp12MaxDiff(1);
if (alg == STEREO_HH)
sgbm->setMode(StereoSGBM::MODE_HH);
else if (alg == STEREO_SGBM)
sgbm->setMode(StereoSGBM::MODE_SGBM);
else if (alg == STEREO_3WAY)
sgbm->setMode(StereoSGBM::MODE_SGBM_3WAY);
C.建立三维结构
通过左右立体像对匹配后,再经过三角测量法来进行立体探测(两角夹一边 -> 确定一个三角形 -> 该三角形的高即为影像点的深度)。与传统的纯双目只需使用两颗普通PRG摄像头,并不涉及光学系统,成本低;测量距离长。
双目立体视觉技术利用双摄像头摄取两幅图像的视差,构建三维场景,在检测到目标后,通过计算图像对应点间位置偏差,获取目标的三维信息,并能以三维立体视角精确区分行人和干扰物体,如推车、行李箱。
具体步骤如下:首先输入原始图,相机标定后得到的内参,以及立体匹配后得到的视差图,再由公式计算出深度图得到Z坐标,并由深度图计算出每个点的X,Y坐标,最后由原始图和计算出的(X,Y,Z)生成并显示点云。
结果
我们在无人机上固定好了双目相机组,在我们使用无人机进行航拍后,得到了一组航拍图像,再通过上述处理过程对组图进行处理后,得到的三维模型如图所示。目前我们只显示出了三维点云,显示效果仍只是个雏形,接下来我们将进行纹理映射工作,让搭建出的环境更加逼真。

问题
此次建模是不单单基于Opencv完成的,还必须基于PCL生成点云完成建模,。为了节省ARM板空间,我们打算只用opencv完成三维重建。而且,由于系统支持的摄像头像素较差,环境苛刻使得拍摄过程中会出现反光等不利因素,从而导致了我们所提取出来的视差图效果不是很理想,因此,通过视差图我们并不能得到非常良好的深度信息。为了解决这个问题,我们目前的思路就是通过特征点提取,获得每一个点的深度信息,着重于提取特征信息视觉深度,从而达到更好的三维重建效果。
左相机内参数矩阵:
[818.1427496880933, 0, 323.0385178639263;
0, 817.9300827874146, 240.8374341990319;
0, 0, 1]
左相机畸变系数:
[0.007972794169599078, 0.9671128656101282, -0.004508405370384771, -0.003759170785283997, -3.974751183062043]
右相机内参数矩阵:
[817.7062598353203, 0, 315.0602094509645;
0, 818.1971497220782, 251.3193229387233;
0, 0, 1]
右相机畸变系数:
[-0.03106127369807768, 1.179919498442583, -0.00365980799250647, -0.002709688952785218, -3.716696603639026]
旋转矩阵:
[ 9.9965083506685637e-01, 8.1936834208969373e-03,
-2.5121136561367424e-02, -9.3036407385304592e-03,
9.9897093188196262e-01, -4.4390534169926173e-02,
2.4731563216770367e-02, 4.4608752581541046e-02,
9.9869835735019297e-01 ]
平移矩阵:
[ -7.1041511229348060e+01, -1.2031693952366919e-01,
-1.9149503217364863e-01 ]
我们的系统是通过两个相机的双目立体视觉对一组图片进行三维重建,为此,在相机组采集到图像后,系统首先将组图分别进行特征点提取,再通过特征点将组图进行立体匹配并对匹配结果进行优化,最后生成对组图进行矫正后的视差图,再根据视差图将原有的图片进行三维拉伸,从而将三维模型搭建起来。